Excel IPMT function is one of the financial functions in Excel, which is used to calculate the interest payment on a loan for a given period. The IPMT function helps users to determine how much of their payment is being applied towards interest and how much is being applied towards the principal balance. It is an essential tool for individuals and businesses to analyze their loan payments and make informed financial decisions.
Excel IPMT Function Summary
The IPMT function in Excel calculates the interest payment for a specific period of a loan. It assumes a constant interest rate and payment amount throughout the entire loan period. The function’s name is derived from “I” for interest and “PMT” for payment, making it easy to remember. Simply input the necessary loan details and the specific payment period to calculate the interest payment for that period.
IPMT Function Purpose
The purpose of the Excel IPMT function is to calculate the interest payment for a given period of a loan.
IPMT Function Arguments
The IPMT function has the following arguments:
- Rate: The interest rate per period.
- Per: The period for which the interest is being calculated.
- Nper: The total number of payment periods.
- Pv: The present value or principal amount of the loan.
- Fv: The future value or the loan balance after the last payment.
- Type: The type of payment at the beginning or end of the period.
IPMT Function Return Value
The IPMT function returns the interest payment for a given period of a loan.
IPMT Function Syntax
The syntax for the IPMT function is:
=IPMT(rate, per, nper, pv, [fv], [type])IPMT Formula for Different Payment Frequencies
When calculating loan payments, it’s important to consider the payment frequency, as this can impact the amount of interest paid over time. The Excel IPMT function is a useful tool for calculating the interest portion of a loan payment, and it can be adjusted to account for different payment frequencies.
Here’s a table outlining the IPMT formula for different payment frequencies:
| Payment Frequency | Formula |
|---|---|
| Weekly | =IPMT(rate/52,per52,pmt52,pv) |
| Bi-weekly | =IPMT(rate/26,per26,pmt26,pv) |
| Semi-monthly | =IPMT(rate/24,per24,pmt24,pv) |
| Monthly | =IPMT(rate/12,per12,pmt12,pv) |
| Quarterly | =IPMT(rate/4,per4,pmt4,pv) |
In each formula, “rate” represents the interest rate, “per” represents the period for which interest is being calculated, “pmt” represents the regular loan payment amount, and “pv” represents the loan principal.
By using the appropriate formula for the payment frequency, you can accurately calculate the interest portion of each loan payment and better understand the total cost of borrowing.
So let’s use the table in a real life situation.
Suppose you have taken out a loan of $100,000 at an annual interest rate of 5%, with a term of 20 years and payments made monthly. You want to know the interest portion of the third payment.
Using the IPMT formula with the following inputs:
- Rate: 5%/12
- Nper: 2012
- Pv: -100000
- Fv: 0
- Type: 0
- Per: 3
We can calculate the interest portion of the third payment:
- Interest portion = -IPMT(5%/12, 3, 2012, -100000, 0, 0)
- Interest portion = $416.67
This means that the third payment includes $416.67 of interest. The remaining portion of the payment goes towards paying down the principal amount of the loan.
IPMT Function Examples
The Excel IPMT function is a useful tool for calculating the interest payment on a loan for a given period. It helps to determine how much of a payment is being applied to the interest, as opposed to the principal. Here are some examples of how the IPMT function can be used:
Simple Interest Calculation
Suppose you have a loan with a principal of $10,000, an annual interest rate of 5%, and a term of 5 years. You want to know how much of the first monthly payment of $188.71 is applied to the interest.
To calculate this, you can use the formula:
=IPMT(5%/12, 1, 5*12,A2)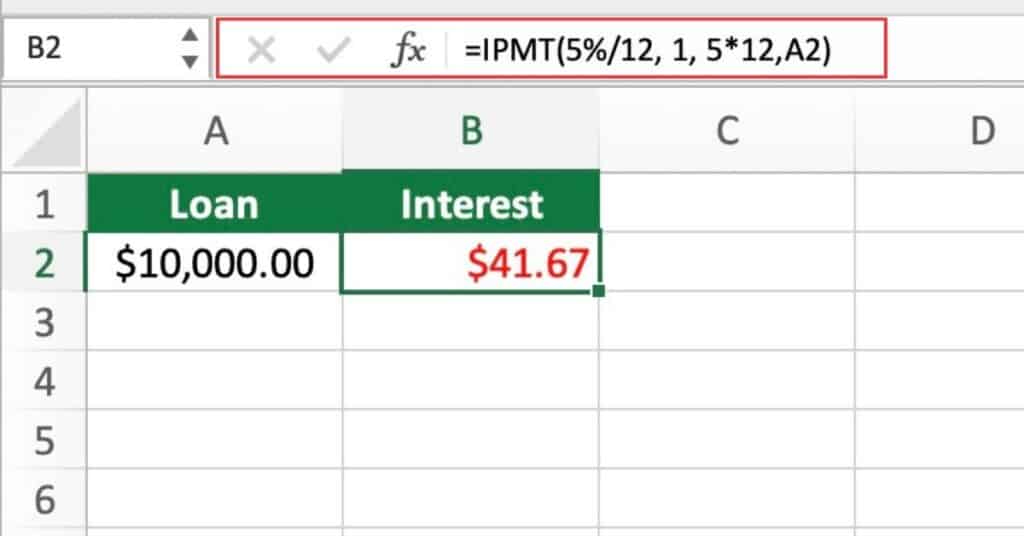
which will return $41.67, the interest payment for the first month.
Amortization Schedule
An amortization schedule shows the breakdown of each payment into its principal and interest components, as well as the remaining balance on the loan. The IPMT function can be used to generate such a schedule.
For example, suppose you have a loan of $50,000 with an annual interest rate of 4% and a term of 10 years. You want to generate an amortization schedule for the first year.
You can use the formula:
=IPMT(4%/12, 1, 10*12, 50000)This will get the interest payment for the first month, and then copy the formula for the remaining 11 months to get the complete schedule.
Variable Interest Rate
The IPMT function can also be used to calculate the interest payment on a loan with a variable interest rate. For example, suppose you have a loan with a starting principal of $20,000, an initial interest rate of 3%, and a term of 5 years. However, after the first year, the interest rate will increase by 1% each year. You want to know the interest payment for the second year.
You can use the formula:
=IPMT((3%+1%)/12, 13, 5*12, 20000)This formula will get the interest payment for the 13th month (i.e., the second year).
Calculating the Interest Payment for a Specific Period
Suppose you take out a loan of $10,000 at a 5% annual interest rate for five years. You want to determine the interest paid for the second year of the loan. To calculate this, you can use the IPMT function as follows:
=IPMT(5%/12, 24, 60, 10000)Calculating the Total Interest Paid for the Loan:
To calculate the total interest paid for the loan, you can use the IPMT function in a loop to calculate the interest paid for each period and then sum up the results.
Suppose you take out a loan of $10,000 at a 5% annual interest rate for five years. To calculate the total interest paid over the life of the loan, you can use the following formula:
=SUMPRODUCT(IPMT(5%/12, ROW(INDIRECT("1:"&60))), -1)IPMT Function Notes
- The IPMT function assumes that payments are made on a regular schedule, such as monthly or annually.
- The IPMT function returns a negative value because it represents an expense.
- The PV and FV arguments must have the same sign, either both positive or both negative.
